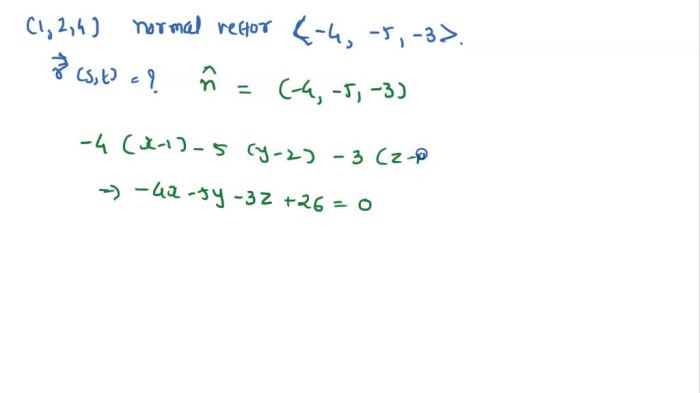Parameterize the plane through the point with the normal vector – In geometry, parameterizing a plane is a fundamental concept that allows us to represent and analyze planes using algebraic equations. In this article, we delve into the process of parameterizing a plane through a given point with a specified normal vector, exploring its significance, geometric interpretation, and wide-ranging applications.

By understanding the parameterization of planes, we gain a powerful tool for solving geometric problems, modeling surfaces, and analyzing geometric relationships in various fields such as computer graphics, engineering, and physics.

Parameterization of a Plane: Parameterize The Plane Through The Point With The Normal Vector

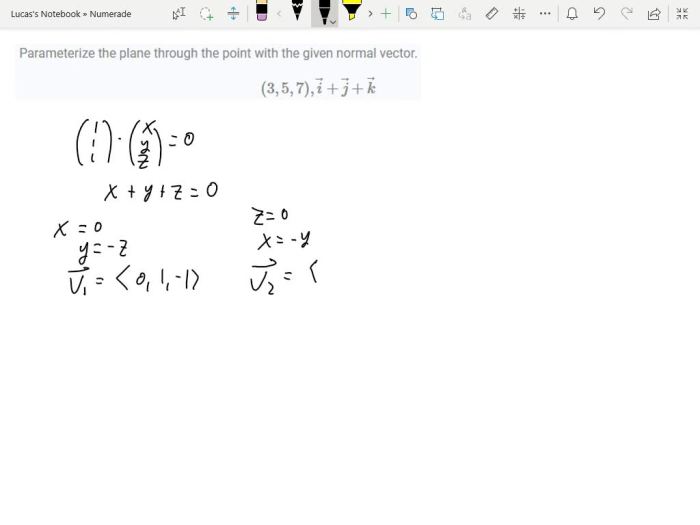
In geometry, a plane can be defined by its normal vector and a point lying on the plane. Parameterizing a plane involves expressing the points on the plane in terms of two parameters. This representation provides a systematic way to describe the geometry of the plane and facilitates various geometric operations.

Plane through a Point with Normal Vector

To parameterize a plane through a given point with a specified normal vector, we can use the following steps:

1. Let \(P_0 = (x_0, y_0, z_0)\) be the given point on the plane.
2. Let \(n = (a, b, c)\) be the given normal vector to the plane.
3. Let \(u\) and \(v\) be two parameters.
4. Define a vector \(v = (u, v, 0)\) lying on the plane.
5. The position vector of any point \(P\) on the plane can be expressed as:$$P = P_0 + v = (x_0, y_0, z_0) + (u, v, 0) = (x_0 + u, y_0 + v, z_0)$$

This parameterization generates all points on the plane that pass through the point \(P_0\) and are parallel to the normal vector \(n\).

Vector Representation of a Plane

The normal vector and a point on the plane can be used to represent the plane in vector form. The vector equation of a plane is given by:

$$\vecr \cdot \vecn = d$$

where:

• \(\vecr\) is the position vector of any point on the plane.
• \(\vecn\) is the normal vector to the plane.
• \(d\) is the signed distance from the plane to the origin.

The vector representation of a plane provides a concise and convenient way to analyze the geometric properties of the plane.

Parametric Equations of a Plane, Parameterize the plane through the point with the normal vector

The parametric equations of a plane through a given point with a specified normal vector are obtained by substituting the parameterization into the vector equation of the plane. The parametric equations are given by:

$$x = x_0 + au$$$$y = y_0 + bv$$$$z = z_0$$

where \(u\) and \(v\) are the parameters.

The parametric equations provide an explicit description of the points on the plane and are useful for solving geometric problems involving planes.

Applications of Parameterized Planes

Parameterized planes find applications in various fields, including:

• Computer graphics:Modeling surfaces and generating realistic images.
• Engineering:Designing and analyzing structures, such as bridges and buildings.
• Physics:Describing the motion of objects and analyzing physical phenomena.

By parameterizing planes, we can perform complex geometric calculations, analyze spatial relationships, and model real-world objects and phenomena.

Helpful Answers

What is the significance of parameterizing a plane?

Parameterizing a plane allows us to represent it algebraically using equations, making it easier to analyze its properties, perform calculations, and solve geometric problems involving the plane.

How is a plane represented in vector form using its normal vector and a point on the plane?

The vector representation of a plane is given by the equation: n · (x – p) = 0, where n is the normal vector, p is a point on the plane, and x is any point in space.

What are the advantages of using parametric equations to describe a plane?

Parametric equations provide a flexible way to represent a plane by varying parameters, allowing us to generate points on the plane and explore its geometry in a systematic manner.